Subject: Physics
Class XI
Time Allowed: 3 hours
Max. Marks: 70
General Instructions:
(1) There are 35 questions in all. All questions are compulsory.
(2) This question paper has five sections: Section A, Section B, Section C, Section D and Section E. All the sections are compulsory.
(3) Section A contains eighteen MCQ of 1 mark each, Section B contains seven questions of two marks each, Section C contains five questions of three marks each, section D contains three long questions of five marks each and Section E contains two case study based questions of 4 marks each.
(4) There is no overall choice. However, an internal choice has been provided in section B, C, D and E You have to attempt only one of the choices in such questions.
(5) Use of calculators is not allowed.
SECTION – A
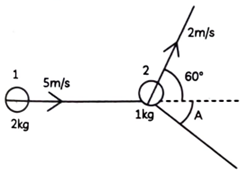
1. Ball 1 has an initial velocity of 5m/s in the diagram. Initially, Ball 2 is at rest. Ball 2 moves at a speed of 2m/s in the direction depicted after collision, while ball 1 moves at an angle ofA. What is the angle A’s value?
a) tan ⁻¹ 1/√3
b) sin ⁻¹ 1/3√3
c) tan ⁻¹ 1/3√3
d) tan ⁻¹ √3
2. When a load W is hung from a wire connected to a roof, it elongates by l mm. If the wire is passed through a pulley and two weights W each are hung at both ends, the wire’s elongation will be (in mm):
a) Zero
b) l
c) l/4
d) l/2
3. A weight of caravan having 1500kg which is running with a velocity 60km/hr on flat horizontal rails. A mass of weight 300 kg is dropped into it. Calculate the final velocity with which it runs now is:
a) 25 km/h
b) 50 km/h
c) 40 km/h
d) 20 km/h
4. In one dimensional motion, instantaneous speed v satisfies 0 ≤ v ≤ vo Then:
a) displacement in time T must always take non-negative values
b) displacement x in the time T satisfies – vo T < x < vo T
c) acceleration is always a non-negative number
d) Motion has no turning points.
5. A ball is travelling with uniform translator motion. This means that,
a) It is at rest
b) The path can be a straight line or circular and the ball travels with uniform.
c) all parts of the ball have the same velocity (magnitude and direction) and the velocity is constant.
d) The center of the ball moves with constant velocity, and the ball spins about its center uniformly.
6. A car of mass m starts from rest and acquires a velocity along east (v > 0) in two seconds. Assuming the car moves with uniform acceleration, the force exerted on the car is
a) eastward and is exerted by the car engine
b) Eastward and is due to friction on the tires exerted by the road.
c) More than eastward exerted due to the engine and overcomes the friction of the road.
d) Exerted by the engine.
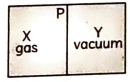
7. A confined flask is completely sealed off from the outside world. As shown in the diagram, one half it is filled with an ideal gas X, separated from the other half Y by a plate P, which contains a vacuum. X enters Y when O is removed. Which of the following statements is NOT correct?
a) No work is done by X
b) X decreases in temperature
c) X increases in internal energy
d) X doubles in pressure
8. If momentum (P), area (A) and time (T) are taken to be fundamental quantities, then energy has the dimensional formula:
a) (P1 A⁻¹ T¹)
b) (P² A² T¹)
c) (P¹ A-1/2 T¹)
d) (p¹ A1/2 T⁻¹)
9. We have two forces having same magnitude F, which acts on an object and the magnitude of the resultant force is F/4. The angle between these two forces:
a) Cos ⁻¹ (31/32)
b) cos ⁻¹ (32/31)
c) cos ⁻¹ (8/9)
d) cos ⁻¹ (2/3)
10. The equation x = 5.0 cos (2πt + π) describes how a body oscillates with SHM. Its displacement, speed and acceleration are as follows at time t = 1.5 s:
a) 0, -10 π, + 20 π²
b) 5, 0, -20 π²
c) 2.5, + 20 π, 0
d) -5.0, +5π, -10 π²
11. A railway engine of mass 12,000 kg is moving at a constant of 5ms up an inclined plane of 15° Calculate the power of the engine, given g 9.8 ms⁻².
a) 152.19 W
b) 140.29 W
c) 129.29 W
d) 119.59 W
12. While washing dirty clothes lots of detergent is kept inside a wash tub for removing dirt or greasy strains this is done due to many reasons; some are stated below. Check each statement and find whether it is correct or not;
(i) it raised the oil-water surface tension
(ii) it reduces the surface tension of oil in water
(iii) it causes the solution’s viscosity to rise.
(iv) Dirt is held suspended by detergent molecules.
a) (i) and (ii)
b) (i) only
c) (iii) and (iv)
d) (iv) only
13. Sound waves of wavelength l traveling in a medium with a speed of v m/s enter into another medium where its speed is 2v m/s wavelength of sound waves in the second Y medium is
a) λ
b) λ/2
c) 2λ
d) 4λ
14. A physical quantity is measured and the result is expressed as nu where, u is the unit used and n is the numerical value. If the result is expressed in various units, then
a) n ∝ size of u
b) n ∝ u²
c) n ∝ √u
d) n ∝ 1/u
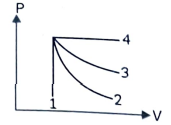
15. An ideal gas undergoes four different processes from the same initial state (figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3, and 4 which one is adiabatic?
a) 4
b) 3
c) 2
d) 1
Two statements are given-one labelled Assertion (A) and other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true and R is not the correct explanation of A
c) A is true but R is false
d) A is false and R is also false
16. Assertion (A): A body can have acceleration even if its velocity is zero at a given instant.
Reason (R): A body is momentarily at rest when it reverses its direction of velocity.
a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true and R is not the correct explanation of A
c) A is true but R is false
d) A is false and R is also false
17. Assertion (A): The front of an automobile is designed to resemble the flow line pattern of the fluid through which it moves.
Reason (R): The shape of an automobile is streamlined to reduce the resistance provided by the fluid.
a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true and R is not the correct explanation of A
c) A is true but R is false
d) A is false and R is also false
18. Assertion (A): The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason (R): The value of acceleration due to gravity is minimum at the equator and maximum at the pole.
a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true and R is not the correct explanation of A
c) A is true but R is false
d) A is false and R is also false
SECTION – B
19. Suppose there existed a planet that went around the sun twice as fast as the earth. What would be its orbital size as compared to that of the earth?
Ans. Lesser by a factor of 0.63
Time taken by the Earth to complete one revolution around the Sun, Te = 1 year
Orbital radius of the Earth in its orbit, Re = 1 AU
Time taken by the planet to complete one revolution around the Sun, Tp = ½ Te = ½ year
Orbital radius of the planet = Rp
From Kepler’s third law of planetary motion, we can write:
(Rp/Re)³ = (Tp/Te)²
Rp/Re = (Tp/Te)2/3
(½/1)2/3 = (0.5)2/3
0.63
Hence the orbital radius of the planet will be 0.63 times smaller than that of the Earth.
20. A system goes from P to Q by two different paths in the P – V diagram as shown in figure. Heat given to the system in path 1 is 1000 J. The work done by the system in path 1 is more than 2 by 100 J. What is the heat exchanged by the system in path 2?
Ans. For path (1)
Q₁ = +1000 J
Work done = W₁ – W₂ = 100
W₁ = WD through path 1
W₂ = WD = through path 2
W₂ = W₁ – 100
As change in internal energy by path 1 and 2 are same
ΔU = Q₁ – W₁ = Q₂ – W₂
1000 – W₁ = Q₂ – (W₁ – 100)
1000 = Q₂ + 100
Q₂ = 900 J
21. A juggler maintains four balls in motion, making each in turn rise to a height of 20 m from his hand. With what velocity does he project them, and where will the other three balls be at the instant when the fourth one is just leaving the hand?
Ans. For the upward motion of a ball:
V = 0, a = -10m/s², s = 20 m, u = ?, t = ?
As v² – u² = 2as
0 – u² = -2 x 10 x 20
u = 20 m/s
Also v = u + at
0 = 20 – 10t
t = 2 s
So the ball returns to the hand of the juggler after 4 s.
To maintain proper distance, the balls must be thrown up at an interval of 4/4 = 1 s
When the fourth ball is in hand, the third ball has travelled for 1 s, second for 2 s, and first for 3 s.
(i) For third ball, s = ut + ½ at²
= 20 x 1 – ½ x 10 x 1 x 1 = 15 m
(ii) For the second ball, s = ut + ½ at²
20 x 3 – ½ x 10 x 3 x 3 = 15 m
OR
When a block is released from the top, it slides down a smooth inclined plane, while another ball falls freely from the same position. Which of them will fall to the ground first?
Ans. Acceleration of the freely falling block is g while that of the block sliding down the smooth inclined plane is where θ is the angle of inclination. On the other hand, the acceleration of the freely falling body is g. Since g > g sin θ, so the block falling freely will reach the ground earlier.
22. A wave propagates down a long rope, which hangs freely from a support. As it propagates, what happens to the speed of the wave?
Ans. A wave can be thought of as a disturbance or oscillation that travels through space-time, accompanied by a transfer of energy. The direction a wave propagates is perpendicular to the direction it oscillates for transverse waves. A wave does not move mass in the direction of propagation; it transfers energy. The speed of a pulse or wave on a strong under tension can be given as;
v = √(T/μ)
where, μ is mass per unit length of rope.
At a distance x from the lower end, we will find tension which will be T = μgx, so, equation will become
v = √(μgx/μ) = √gx
23. A gaseous mixture consists of 2.0 moles of oxygen and 4.0 moles of neon at temperature T neglecting all vibrational modes, calculate the total internal energy of the system (Oxygen has two rotational modes)
Ans. Oxygen is a diatomic molecule, i.e., a molecule of oxygen of two atoms of oxygen. So, it has 5 degrees of freedom (3 due to translation motion and 2 due to rotational motion). The total energy of 2 moles of oxygen is:
E₁ = 5/2 x 2 x RT
= 5RT
Similarly, neon is monatomic (contains a single atom) and thus has 3 degrees of freedom, outgoing to its translation motion only.
So. Total energy of 4 moles of neon gas is
E₂ = 3/2 x 4 x RT
= 6RT
The total internal energy of the gaseous mixture is equal to
E = E₁ + E₂
= 5RT + 6RT
= 11RT
24. The graph between the resistive force F acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 25 kg and the initial velocity is 2 m/s. When the distance covered by the body is 5 m. then find its kinetic energy.
Ans. Initial kinetic energy of the body
½ x mu² = ½ x 25 x 2²
= 50 Joule
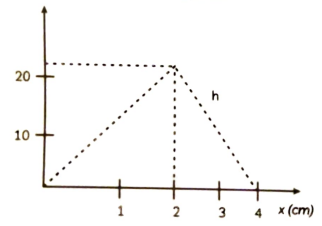
Final kinetic energy = Initial kinetic energy – work done against resistive force (Area between graph and displacement axis)
= 50 – ½ x 4 x 20
= 50 – 40 = 10 J
OR
A wheel is rotating with angular velocity 2 rad/s. It is subjected to a uniform angular acceleration 2.0 rad/s²
A) What angular velocity does the wheel acquire after 10s?
Ans. The wheel is in uniform angular acceleration. Hence
ω = ω₀ + αt
On substituting the values of ω₀, α and t, we have
Ω = 2 x 2 x 10 = 22 rad/s
Θ = θ₀ x ½(2 + 22) 10 = 120 rad
B) How many revolutions will it make in this time interval?
Ans. In one revolution, the wheel rotates through 2π radians. Therefore, the number of complete revolutions n is
M = θ/2π = 120/2π = 19
25. A laser beamed at the Moon takes 2.56 s to return after reflection at the Moon’s surface. How much is the radius of the lunar orbit around the Earth?
Ans. A LASER is a source of a very intense, monochromatic and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. Time taken by the laser beam to return to Earth after reflection from the Moon = 2.56 s
Speed of light 3 x 10⁸ m/s
Time taken by the laser beam to reach Moon
= ½ x 2.56 = 1.28 s
Radius of the lunar orbit = Distance between the Earth and the Moon
= 1.28 x 3 x 10⁸ = 3.84 x 10⁸ m
3.84 x 10⁵ km
SECTION – C
26. A man weighing 80 kgf carries a stone of weight 20 kgf to the top of the building 30 m high. Calculate the work done by him. Given g = 9.8 ms⁻²
Ans. Here weight of man = 80kgf
Weight of stone = 20 kgf
Force applied to carry the total weight up
F = 80 + 20 = 100 kgf
= 100 x 9.8
= 980N
Height through which the weight is carried
S = 30 m
Work done W = Fs = 980 x 30 = 23,400J
27. There are n gas molecules in the container. If you increase the number of molecules to 2n, what will be:
A) Gas pressure?
Ans. We know that p = 1/3 mnc²
Where, n = number of molecules per unit volume
Thus, when number of molecules is increased from n to 2n, number of molecules per unit volume (n) will increase from n to 2n.
B) Total gas energy?
Ans. The K.E of a gas molecule is
½ mc² = 3/2 kT
If the number of molecules is increased from n to 2n. There is no effect on the average K.E of a gas molecule, but the total energy is doubled.
C) RMS rate of gas molecules?
R.M.S speed of gas is vrms = √(3P/P) = √(3P/mn)
Where n is increased from n to 2n both n and P become double and the ratio P/n remains unchanged. So there will be no effect of increasing the number of molecule from n to 2n on rms speed of gas molecules.
28. In the given figure gives the x – t plot of a particle executing one – dimensional simple harmonic motion. Give the signs of position, velocity, and acceleration variables of the particle at t = 0.3 s, 1.2 s, -1.2 s
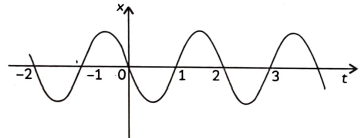
Ans. The acceleration of a particle executing S.H.M. is given by
A = – ω²x
Where ω (angular frequency) is a constant.
At time t = 0.3 s
As is obvious from the graph, x < 0
As slope of x – t graph is negative, so v < 0
As a = – ω²x, so a > 0
At time t = 1.2 s
As is obvious from the graph, x > 0
As slope of x – t graph is positive, so v > 0
As a = – ω²x, so a < 0
At time t = -1.2 s
As is obvious from the graph, x > 0
As slope of x – t graph is positive, so v > 0
As a = – ω²x, so a > 0
29. A jeweler wishes to harden a sample of pure gold by mixing it with some silver so that the mixture contains 5.0% silver by weight. The jeweler melts some pure gold and then adds the correct weight of silver. The initial temperature of the silver is 27°C. Use the data given below to calculate the initial temperature of pure gold, so that the final mixture is at the melting point of pure gold.
Melting point of gold and silver – 1340K and 1240K respectively.
Specific heat of gold and silver = 129 JKg⁻¹K⁻¹ and 235 JKg⁻¹K⁻¹ respectively.
Specific latent heat of fusion of gold and silver = 628 KJKg⁻¹ and 105 KJKg⁻¹ respectively.
Ans. Let T₁ be the initial temperature of pure gold (liquid) and M be the mass of gold and silver mixture.
Then, mass of the gold in the mixture = 0.95 M
Mass of the silver in the mixture = 0.05 M
Here, specific heat capacity of gold
c₁ = 129 J Kg⁻¹K⁻¹
specific heat capacity of silver
c₂ = 235 J Kg⁻¹K⁻¹
Specific latent heat of fusion silver
L₂ = 105 KJKg⁻¹ = 105 x 10³ Jkg⁻¹
Initial temperature of pure silver
T₂ = 27 + 273 = 300K
Final temperature of the mixture, T = 1340K
Heat lost by gold = 0.95 M x c₁ x (T₁ – T)
= 122.55 M x (T₁ – 1340)
Heat lost by silver
= 0.05M x L₂ + 0.05M x c₂ x (T – T₂)
= 5.250M + 12.220 = 17,470
According to principle of calorimetry
122.55 x (T₁ – 1340) = 17,470
T₁ = 1,482.6 K
OR
Figure (a) shows a thin liquid film supporting a small weight = 4.5 x 10⁻² N. What is the weight supported by a film of the same liquid at the same temperature in figure (b) and (c)? Explain your answer physically.
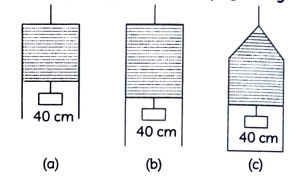
Ans. Length of the film supporting the weight
L = 40 cm = 0.4 m
Total weight supported (i.e., force)
W = 4.5 x 10⁻² N
T = surface tension =?
The film has two free surfaces, so total length
L = 2l = 2 x 0.4 m
T = Force / Length
= (4.5 x 10⁻²)/(2 x 0.4)
= 5.625 x 10⁻² Nm⁻¹
As the liquid is same for all the cases (a), (b) and (c) and temperature is also same, therefore surface tension for cases (b) and (c) will also be the same, i.e., 5.625 x 10⁻² Nm⁻¹.
In figure (b) and (c), the length of the film supporting the weight is also the same as that of (a), hence the total weight supported in each case is 4.5 x 10⁻²
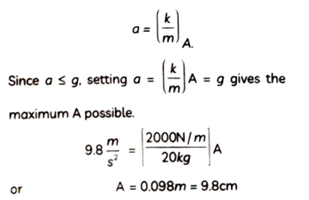
30. A small object is placed on top of a block of mass m 20 kg that is hung from one end of a vertical spring of force constant k = 200ON/m and whose other end is attached to the ceiling. The block is pulled down a distance. A below the equilibrium position and released from rest. What is the maximum value of A for which the small object remains in contact with the block throughout the subsequent SHM?
Ans. Contact will be lost only if the downward acceleration of the block momentarily exceeds the acceleration of gravity g. When that occurs, the object will not be able to follow the motion of the block. The block’s maximum downward acceleration occurs at the highest point in the motion, which corresponds to the amplitude A of motion and is the same as the distance of release below equilibrium. AT this highest point, the acceleration has magnitude
OR
The transverse displacement of a string (clamped at its both ends) is given by,
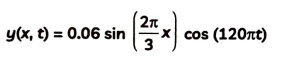
Where x, y are in m and t in s. The length of the string is 1.5 m and its mass is 3 x 10⁻² kg. Answer the following:
A) Does the function represent a travelling or a stationary wave?
Ans. The equation given,
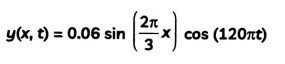
This equation is both harmonic functions of x and t separately. Thus it represents a stationary wave.
B) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength o, frequency and speed of propagation of each wave?
Ans. A stationary wave is formed when a wave
y₁ = a sin 2π/3 (vt – x)
travelling along +ve direction of x and Another reflected wave.
y₂ = – a sin 2π/3 (vt – x) …… (i)
travelling along –ve direction of x, superpose on each other.
Resultant wave
y = y₁ + y₂
= 2a sin 2π/3 cos 2π/3 vt …… (ii)
Comparing equation (i) and (ii)
2πv/3 = 120 π
V = 60 = 60 x 3 = 180 m/s
Frequecy, v = v/3 = 180/3 = 60 Hz
Both waves have same wavelength, frequency and speed
C) Determine the tension in the string?
C) Velocity
V =√(T/m)
T = v² x m
= (180) ² x 3 x 10⁻²/1.5
= 648 N
SECTION – D
31. Two bodies having unequal masses which are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying a force of the same magnitude. How would the distance moved by them before coming to rest compare?
Ans. Let the two bodies be of masses M1 and M2 and moving with speeds u1 and u2 respectively. Since they have equal kinetic energy
1/2M1u1² = 1/2M2u2²
Or u1²/u2² = M1 = M2 ….. (1)
When the same retarding force F is applied on the two bodies, suppose that they come to rest by covering distances S1 and S2 respectively. If a1 and a2 are the retardation respectively, then
M1a1 = M2a2
Or
A1/a2 = M1/M2 ….. (2)
Now, v² – u² = 2as
For the first day
(0)² – u1² = 2(-a1)s1
Or u1² = 2a1s1
Similarly for the first body
U2² = 2a2s2
U1²/u2² = a1s1/a2/s2
Using equation (1) and (2) the equation (3) given s1 = s2 i.e., the two bodies will come to rest within the same distance.
OR
A satellite is to be placed in equatorial geostationary orbit around earth for Communication.
A) Calculate height of such a satellite.
Ans. mass of earth M = 6 x 10²⁴ kg
Radius of the earth R = 6400 km = 6.4 x 10⁶ m
Time period T = 24 h = 24 x 3600
S = 24 x 36 x 10²
G = 6.67 x 10⁻¹¹N-m⁻² kg⁻²
Orbital Radius = (R + h)
h is height of satellite from earth surface
vo = √[GM/(R + h)]
vo² = GM /(R + h)
T = 2 π(R + h)/vo
h = 35,940 km
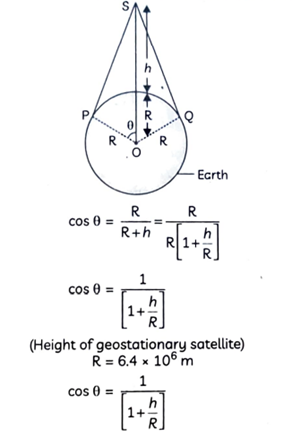
B) Find out the minimum number of satellite that are needed to cover entire earth so that at least one satellite is visible from any point on the equator.
[M = 6 x 10²⁴ Kg, R = 6400 km, T = 24 h, G = 6.67 x 10⁻¹¹ SI Units]Ans. Let a satellite S is at hm above the earth surface. Let angle subtended by satellite at centre of earth 2. Then in right angle ΔSPO

32. A cyclist is travelling at a speed of 27 kilometers per hour. As he approaches a circular turn on a road with a radius of 80 metres, he hits the brakes and slows down at a steady pace of 0.50 metres per second. What is the magnitude and direction of the cyclist’s net acceleration during a circular turn?
Ans. 54.46° with the direction of velocity
Speed of the cyclist, v = 27 km/hr = 7.5 m/s
Radius of the circular turn, r = 80 m
Centripetal acceleration is given as:
Ac = v²/r = (7.5)²/80 = 0.2 ms⁻²
The situation is shown in the given figure
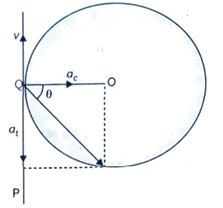
Suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the brakes and decelerates the speed of the bicycle by 0.5 m/s².
This acceleration is along the tangent at Q and opposite to the direction of motion of the cyclist. Since the angle between ac and at is, the resultant acceleration a is given by
a = √(ac² + at²) = √ [(0.7)² + (0.5)²] = √0.74
= 0.86 m/s²
tan θ = ac/at = 0.7/0.5 = 1.4
θ = tan⁻¹ (1.4) = 54.46°
OR
The greatest height to which a boy throws a ball is 50 m. What will be the greatest distance along the horizontal up to which the boy can throw the ball with the same speed?
Ans. It is given that the boy can throw a stone to a maximum height of 50 m
To throw a stone to maximum height, the boy has to throw the stone vertically upwards.
Third equation of motion: v² = u² + 2as
Final velocity of the ball, v = 0
Acceleration of the ball = – Acceleration due to gravity = -g
Displacement of the ball, s = 50 m
Putting all these values to the third equation of motion, we get
0 = u² – 2g x 50 …… (1)
Maximum range Rmax = 100g/g = 100 m
Now, maximum height for maximum range
Hmax = u²/2g sin θ
Putting values in above equation, we get 3 θ = 45, for maximum range
Hmax = 50/2 = 25 m
Hence, maximum range of the ball is 100 m and greatest height for maximum range is 25 m.
33. For the given figure shown (a) and (b) the solid block represents the equilibrium position and the dashed-line block represents its position after a displacement x from equilibrium. For each case, find the equivalent force constant of a single spring that would have the same effect on the block, thus showing that the block undergoes SBH, find the period of SHM for each case.
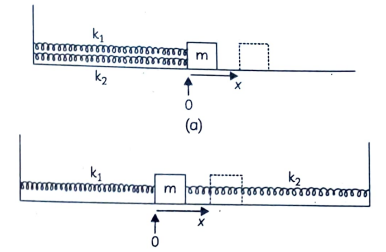
For fig (a), in stretching to position x from equilibrium, the restoring force to the left due to both springs is F = -k1x – k2x = -(k1 + k2)x
The equivalent single spring would give a force
Thus F = -kx
k = k1 + k2
and R = 2π√[m/(k1 + k2)]
For figure (6), Here the two springs are pulling in opposite directions and just balance at the equilibrium position. If the block is pulled a distance x to the right of equilibrium, then spring one will increase its pull to the left by k1 x, while spring two will decrease its pull to the right by k2 x. Therefore, the net force at position x is k1x + k2x to the left. Then, the equivalent single spring will again have force constant.
k = k1 + k2
and T = √[m/(k1 + k2)]
OR
In given progressive wave
y = 5 sin (100πt – 0.4 πx),
Where x, y is in m and t in seconds.
What is the:
A) Amplitude
Ans. Standard form of progressive wave traveling in + x direction (kx and ωt have opposite sign is given) eqn is y = a sin (ωt – kx + Ø)
y = 5 sin (100πt – 0.4 πx)
Amplitude a = 5 m
B) wavelength
Ans. Wavelength λ
k = 2π/ λ
k = 0.4π
λ= 2 π/k = 2 x π/0.4 π = 5 m
C) Frequency
Ans. ω = 2πv
v = ω/2π
v = 100 π/2π = 50 Hz
D) wave velocity
Ans. v = v = 50 x 5
= 250 m/s
E) Particle velocity amplitude?
Ans. Particle (medium) velocity in the direction of amplitude at a distance x from source.
y = 5 sin (100πt – 0.4 πx)
dy/dt = 5 x 100πt – 0.4πx)
For maximum velocity of particle is at its mean position
Cos (100πt – 0.4πx) = 1
100πt – 0.4 πx = 0
(dy/dt)max = 5 x 100π x 1
Vmax of medium particle = 500π m/s
SECTION –E
34. A Cooking utensils are made of metal which has low specific heat capacity so that it need less heat to raise up the temperature. Handles of cooking utensils are made of substances with high specific heat capacities so that its temperature won’t become too high even if it absorbs large amount of heat

A) A tank of volume 0.3 m³ contains 2 moles of Helium gas at 200C. Assuming the helium behave as an ideal gas, what will be the total internal energy of the system?
Ans. n = No of moles = 2
T = temperature = 273 + 20 = 293K
R = Universal Gas constant = 8.31 J/mole
Total energy of the system = E = 3/2 nRT
E = 3/2 x n x 8.31 x 293
E = 7.30 x 10³ J
B) There are two gases named hydrogen and oxygen which are stored in a body. If there is a tiny hole in the box, which gas will discharge very fast? Why?
Ans. We know that vrms π 1/ √Mo
Hence, hydrogen gas will leak more rapidly of its smaller molecular mass.
C) A gas occupies a volume of 400 cm³ at 0 degree Celsius and 780 mm of Hg. How many liters of volume will the gas occupy at so degree Celsius and 780 mm of Hg.
Ans. According to the question,
V₁ = 400 cm³
T₁ = 0°C= 0 + 273 = 273K
T₂ – 80°C= 80 + 273 = 383K
You need to find V₂
Here only the temperature is changing, the pressure remains constant.
Using Charles law V₁/T₁ = V₂/T₂
Putting the above values in the Charle’s law, we get
400/273 = V₂/353
V₂ = 517.21 cm³
Since 1 cm³ = 0.001 litres,
Then 517.21 cubic cm = 517.21 x 10³ = 0.517L
OR
At very low pressure and high temperature, the real gas behaves like ideal gas. Why?
Ans. An ideal gas is one which has zero volume of molecule and no intermolecular forces. Now
(i) At very low pressure, the volume of gas is large so that the volume of molecule is negligible compared to volume of gas.
(ii) At very high temperature, the kinetic energy of molecules is very large and effect of intermolecular forces can be neglected.
Hence real gases behave as an ideal gas at low pressure and high temperature.
35. Every particle of a rotating body moves in a circle. The linear velocity of the particle is related to the angular velocity. The relation between these two quantities involves a vector product for rotation about a fixed axis, the direction of the vector w does not change with time. Its magnitude may, however, change from instant to instant. For the more general rotation, both the magnitude and the direction of ω may change from instant to instant.
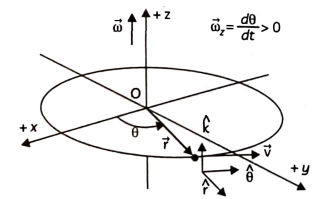
A) What is the angular velocity of a bike wheel if it takes 3 seconds to complete one revolution?
Ans. The definition of angular velocity is
ω = Δθ/Δt
By identifying the given information to be Δθ = 2 π and Δt = 3s, we can plug this into the equation to calculate the angular velocity
ω = 2 π/3s = 2.09s⁻¹
B) Explain with reason why a ballet dancer varies her angular speed by outstretching her arms and legs.
Ans. Ballet dancer while performing fold her arms to spin faster. Thus, act involves the use of rotational motion i.e., when the dancer folds her arm while spinning the moment of inertia decreases. As L = l ω. To keep the L constant, the angular velocity ω increases and hence ballet dancer spins faster there by enhancing the performance.
C) A 95 kg person is riding a Ferris wheel with a radius of 10 m. The wheel rotates at a constant angular rate of one revolution per minute. Determine the rider’s linear velocity.
Ans. Convert rotations/minute to meters/second
1 rotations/minute x 1 minute/60 seconds
= 2 x π x 10 metres/1 rotations = 1.05 metres/ second
OR
Two men stand facing each other on two separate boats drifting on quiet water. Both are holding the end of a rope. Why do the two boats always meet at the same location, whether each guy pulls alone or both full together? Will the time taken in the two scenarios be different? Ignore friction.
Ans. The men on the two boats floating on water constitute a single system. So, the forces applied by the two men are internal forces. Whether each man pulls separately or both pull together, the centre of mass of the system of boats remains fixed due to the absence of any external forces. Consequently, the two boats meet at a fixed point, which is the centre of mass of the system.