Subject: Mathematics (Basic)
Class X
Time Allowed: 3 hours
Max Marks: 80
General Instructions:
1. This Question Paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each
3. Section B has 5 questions carrying 02 marks each.
4. Section C has 6 questions carrying 03 marks each.
5. Section D has 4 questions carrying 05 marks each.
6. Section E has 3 case based integrated units of assessment (04 marks each) with sub-parts of the values of 1, 1 and 2 marks each respectively.
7. All Questions are compulsory. However, an internal choice in 2 Qs of 5 marks, 2 Qs of 3 marks and 2 Questions of 2 marks has been provided. An internal choice has been provided in the 2marks questions of Section E
8. Draw neat figures wherever required. Take 7 22 π = wherever required if not stated.
SECTION A
Section A consists of 20 questions of 1 mark each.
1. The maximum number of zeroes a cubic polynomial can have, is
(a) 1
(b) 4
(c) 2
(d) 3
View AnswerAns. (d)
2. A fraction becomes 4 when 1 is added to both the numerator and denominator and it becomes 7 when 1 is subtracted from both the numerator and denominator. The numerator of the given fraction is
(a) 2
(b) 3
(c) 5
(d) 15
View AnswerAns. (d)
3. If the point P (6, 2) divides the line segment joining A(6, 5) and B (4, y) in the ratio 3 1: then the value of y is
(a) 4
(b) 3
(c) 2
(d) 1
View AnswerAns. (d)
4. If x – 2y + k = 0 is a median of the triangle whose vertices are at points A (- 1, 3), B (0, 4) and C (-5, 2), then the value of k is
(a) 2
(b) 4
(c) 6
(d) 8
View AnswerAns. (d)
5. The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution, if
(a) k ≠ – 3
(b) k ≠ – 2/3
(c) k ≠ 5
(d) k ≠ 2/9
View AnswerAns. (a)
6. The linear factors of the quadratic equation x2 + kx + 1 = 0 are
(a) k ≥ 2
(b) k ≤ 2
(c) k ≥- 2
(d) 2 ≤ K ≤ -2
View AnswerAns. (d)
7. A circle artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground, then the height of pole, if the angle made by the rope with the ground level is 30°, is
(a) 5 m
(b) 10 m
(c) 15 m
(d) 20 m
View AnswerAns. (b)
8. If the area of a semi-circular field is 15400 sq m, then perimeter of the field is
(a) 160 √2 m
(b) 260 √2 m
(c) 360 √2 m
(d) 460√ 2 m
View AnswerAns. (c)
9. In an AP, if d =− 4, n = 7 and an = 4, then a is equal to
(a) 6
(b) 7
(c) 20
(d) 28
View AnswerAns. (d)
10. The 4th term from the end of an AP -11, -8, -5, ….., 49 is
(a) 37
(b) 40
(c) 43
(d) 58
View AnswerAns. (b)
11. In a right angled Δ ABC right angled at B, if P and Q are points on the sides AB and BC respectively, then

Ans. (C)
12. A chord of a circle of radius 10 cm, subtends a right angle at its centre. The length of the chord (in cm) is
(a) 5/√2
(b) 5 √2
(c) 10 √2
(d) 10 √3
View AnswerAns. (c)
13. If ΔABC is right angled at C, then the value of cos (A + B) is
(a) 0
(b) 1
(c) 1/2
(d) √3/2
View AnswerAns. (a)
14. Ratio of lateral surface areas of two cylinders with equal height is
(a) 1 : 2
(b) H : h:
(c) R : r
(d) None of these
View AnswerAns. (c)
15. For finding the popular size of readymade garments, which central tendency is used?
(a) Mean
(b) Median
(c) Mode
(d) Both Mean and Mode
View AnswerAns. (c)
16. When a die is thrown, the probability of getting an odd number less than 3 is
(a) 1/6
(b) 1/3
(c) 1/2
(d) 0
View AnswerAns. (a)
17. The ratio in which the point (2, y) divides the join of (- 4, 3) and (6, 3), hence the value of y is
(a) 2 : 3, y = 3
(b) 3 : 2, y = 4
(c) 3 : 2, y = 3
(d) 3 : 2, y = 2
View AnswerAns. (c)
18. The sum of exponents of prime factors in the prime-factorization of 196 is
(a) 3
(b) 4
(c) 5
(d) 2
View AnswerAns. (b)
19. Assertion: (2 -√3) is one zero of the quadratic polynomial then other zero will be (2 + √3).
Reason: Irrational zeros (roots) always occurs in pairs.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
View AnswerAns. (a)
20. Assertion: The equation x2 + 3x + 1 = (x – 2)2 is a quadratic equation.
Reason: Any equation of the form ax2 + bx + c = 0 where a ≠ 0, is called a quadratic equation.
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
View AnswerAns. (d)
Section – B
Section B consists of 5 questions of 2 marks each.
21. In Figure ∠D = ∠E and AD/DB = AE/EC, prove that ΔBAC is an isosceles triangle
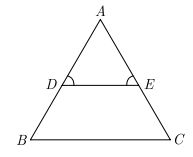
Ans. AD/DB = AE/EC (Given)
Therefore, DE ∥ BC (Converse of Basic Proportionality Theorem)
So, ∠D = ∠B and ∠E = ∠C (Corresponding angles) (1)
But ∠D = ∠E (Given)
Therefore, ∠B = ∠C [ From (1)]
So, AB = AC (Sides opposite to equal angles)
i.e., BAC is an isosceles triangle.
22. In figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + RQ.
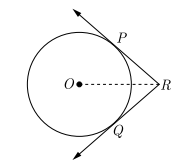
Ans. Join OP and OQ
Given ∠PRQ=120∘
∴∠POQ=60∘ (supplementary angles)
Also, we have PR=RQ (equal tangents) and ∠OPR=90∘ (radii is perpendicular to tangent)
Now,
PR/OR =cos60∘ =1/2 (∠ROP=30∘ and ∠PRO=60∘)
⟹OR=2PR
⟹OR=PR+RQ
Hence proved
23. If √3 sin θ − cos θ = 0 and 0° < θ < 90°, find the value of θ.
View AnswerAns.
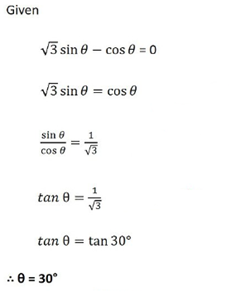
24. Find the value of λ, if the mode of the following data is 20 : 15, 20, 25, 18, 13, 15, 25, 15, 18, 17, 20, 25, 20, λ , 18
View AnswerAns. Writing the data as discrete frequency distribution, we get.

For 20 to be mode of the frequency distribution, λ = 20.
OR
The mean and median of 100 observations are 50 and 52 respectively. The value of the largest observation is 100. It was later found that it is 110. Find the true mean and median.
View AnswerAns. we know that Arithmetic mean =∑X/N
Given Mean =50
N=100
i.e., 50= ∑X/100
∑X=5000
Later found that it is 110
So the 100 items are wrong value
correct A.M = [∑X (wrong) + correct value of observation −
Incorrect value of observation]/N
correct Mean = [5000+110−100]/100
= [5110−100]/100
= 5010/100
=50.10
∴ The real or true mean value is 50.10
Median value is 52
25. Prove that 3 + √5 is an irrational number
OR
Show that any positive even integer can be written in the form 6q, 6q + 2, 6q + 4, where q is an integer.
Section – C
Section C consists of 6 questions of 3 marks each.
26. Show that the sum of all terms of an AP whose first term is a, the second term is b and last term is c, is equal to
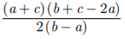
Ans. First term =a
second term =b Last term =c
Difference d=b−a
In an AP, nth term Tn =a+(n−1)d
=a+(n−1)(b−a)
c=a+(n−1)(b−a)
∴c−a=(n−1)(b−a)
∴n−1= (c−a)/(b−a)
∴n= (c−a)/(b−a) +1
Sum of n numbers =n/2 (first term + last term)
=n/2(a+c)
= [((c−a)/(b−a) + 1)(a + c)]/2
= (c−a+b−a)(a+c)/2(b−a)
= (a+c)(b+c−2a)/2(b−a)
27. Prove that (1 + cot A – cosec A)(1 + tan A + sec A) = 2
View AnswerAns.

28. Sides of a right triangular field are 25 m, 24 m and 7 m. At the three corners of the field, a cow, a buffalo and a horse are tied separately with ropes of 3.5 m each to graze in the field. Find the area of the field that cannot be grazed by these animals.
OR
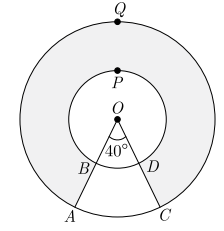
In the given figure, find the area of the shaded region, enclosed between two concentric circles of radii 7 cm and 14 cm where ∠AOC = 40°. Use π = 22/7.
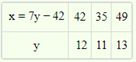
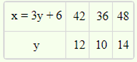
29. The mean of the following distribution is 48 and sum of all the frequency is 50. Find the missing frequencies x and y.

Ans. x= 12, y = 13
30. If the co-ordinates of points A and B are (-2, -2) and (2, -4) respectively, find the co-ordinates of P such that AP =3/7 AB, where P lies on the line segment AB.
View AnswerAns. (-2/7, -20/7)
OR
Find the co-ordinates of the points of trisection of the line segment joining the points A (1, -2) and B (3, 4).
View AnswerAns. The coordinates of the points of trisection of the line segment joining A and B are (-1/3, 0) and (-5/3, 2)
31. Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together?
View AnswerAns. LCM of 9, 12, 15 is 180
Section – D
Section D consists of 4 questions of 5 marks each.
32. Aftab tells his daughter, ‘7 years ago, I was seven times as old as you were then. Also, 3 years from now, I shall be three times as old as you will be.’ Represent this situation algebraically and graphically.
View AnswerAns. Consider Aftab’s age as x and his daughter’s age as y.
Then , seven years ago,
Aftab’s age =x−7
His daughter’s age =y−7
According to the question,
x−7=7(y−7)
x−7=7y−49
x−7y=−49+7
x−7y=−42 …(i)
After three years,
Aftab’s age =x+3
His daughter’s age =y+3
According to the question,
x+3=3(y+3)
x+3=3y+9
x−3y=9−3
x−3y=6 …(ii)
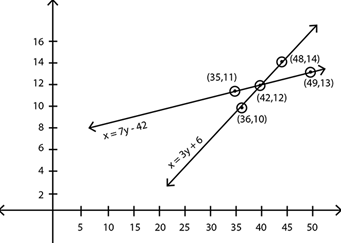
Representing equation (i) and (ii) geometrically, we plot these equations by finding points on the lines representing these two equations
x−7y=−42⟹x=7y−42
x−3y=6⟹x=3y+6
From the graph we can see that two lines will intersect at a point.
x−7y=−42
x−3y=6
On subtracting the two equations, we get
4y=48
or y=12
Substituting value of y in (2),
x−36=6
∴x=42
OR
Solve the following pair of linear equations graphically:
x – y = 1, 2x + y = 8
Also find the co-ordinates of the points where the lines represented by the above equation intersect y – axis.
View AnswerAns.
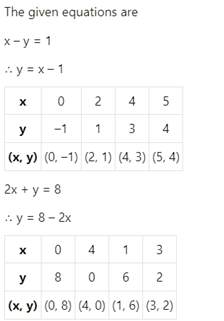
Drawing the graph with the above coordinates.
33. From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
View AnswerAns. A circle with centre O. Tangents TP and TQ are drawn from a point T outside a circle.
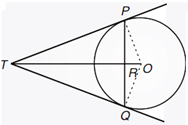
To Prove: OT is the right bisector of line segment PQ.
Construction: Join OP & OQ
Proof: In ∆PTR and ∆QTR
In ∆OPT and ∆OQT
∠OPT = ∠OQT = 90°
OP = OQ (radius)
OT = OT (Common)
∆OPT ≅ ∆OQT (By RHS congruence)
∠PTR = ∠QTR (cpct)
TP = TQ (Tangents are equal)
TR = TR (Common)
∠PTR = ∠QTR (OT bisects ∠PTQ)
∆PTR ≅ ∆QTR (By SAS congruency)
PR = QR
∠PRT = ∠QRT
But ∠PRT + ∠QRT = 180 (as PQ is line segment)
∠PRT = ∠QRT = 90
Therefore, TR or OT is the right bisector of line segment PQ
34. From a point on the ground, the angles of elevation of the bottom and the top of a tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
View AnswerAns.

OR
The angle of elevation of the top B of a tower AB from a point X on the ground is 60°. At point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Find the height of the tower AB and the distance XB.
35. Water is flowing through a cylindrical pipe, of internal diameter 2 cm, into a cylindrical tank of base radius 40 cm, at the rate of 0.4 m/s. Determine the rise in level of water in the tank in half an hour.
Section – E
Case study based questions are compulsory.
36. John and Priya went for a small picnic. After having their lunch Priya insisted to travel in a motor boat. The speed of the motor boat was 20 km/hr. Priya being a Mathematics student wanted to know the speed of the current. So she noted the time for upstream and downstream.

She found that for covering the distance of 15 km the boat took 1 hour more for upstream than downstream.
(i) Let speed of the current be x km/hr. then speed of the motorboat in upstream will be
(ii) What is the relation between speed distance and time?
(iii) Write the correct quadratic equation for the speed of the current?
OR
(iv) What is the speed of current?
37. The centroid is the centre point of the object. It is also defined as the point of intersection of all the three medians. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. The centroid of the triangle separates the median in the ratio of 2 : 1. It can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle.
See the figure given below
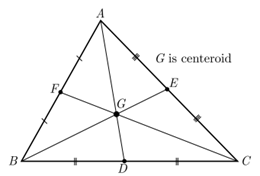
Here D E, and F are mid points of sides BC, AC and AB in same order. G is centroid, the centroid divides the median in the ratio 2 : 1 with the larger part towards the vertex. Thus AG : GD = 2 : 1
On the basis of above information read the question below.
If G is Centroid of ΔABC with height h and J is centroid of ΔADE. Line DE parallel to BC, cuts the ΔABC at a height h 4 from BC. HF =h/4.
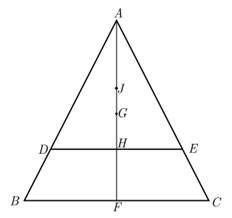
(i) What is the length of AH?
(ii) What is the distance of point A from point G?
(iii) What is the distance of point A from point J?
OR
(iv) What is the distance GJ?
38. Abhinav Bindra is retired sport shooter and currently India’s only individual Olympic gold medalist. His gold in the 10-meter air rifle event at the 2008 Summer Olympics was also India’s first Olympic gold medal since 1980. He is the first Indian to have held concurrently the world and Olympic titles for the men’s 10-meter air rifle event, having earned those honors at the 2008 Summer Olympics and the 2006 ISSF World Shooting Championships. Bindra has also won nine medals at the Commonwealth Games and three gold medals at the Asian Games.

A circular dartboard has a total radius of 8 inch, with circular bands that are 2-inch-wide, as shown in figure. Abhinav is still skilled enough to hit this board 100% of the time so he always score at least two points each time he throw a dart. Assume the probabilities are related to area, on the next dart that he throw.
(i) What is the probability that he score at least 4?
(ii) What is the probability that he score at least 6?
(iii) What is the probability that he hit bull’s eye?
OR
(iv) What is the probability that he score exactly 4 points?