Subject: Mathematics
Class IX
Time Allowed: 3 hours
Max. Marks: 80
General Instructions:
- This Question Paper has 5 Sections A – E
- Section A has 20 MCQs carrying 1 mark each
- Section B has 5 questions carrying 2 marks each
- Section C has 6 questions carrying 3 marks each
- Section D has 4 questions carrying 5 marks each
- Section E has 3 case based integrated units of assessment (4 marks each) with subparts of the values of 1, 1 and 2 marks each respectively
- All questions are compulsory. However, an internal choice in 2 Qs of 5 marks, 2 Qs of 3 marks and 2 Qs of 2 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figure wherever required. Take π = 22/7 wherever required if not stated.
SECTION A
1. The base of an isosceles triangle is 6 cm and each of its equal sides is 5 cm. The height of the triangle is
a) √11 cm
b) 8 cm
c) √30 cm
d) 4 cm
2. PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
a) 23°
b) 41°
c) 67°
d) 18°
3. The perpendicular distance of the point P(-2, -3) from the y-axis is
a) 3 units
b) -2
c) 2 units
d) -3
4. The simples form of
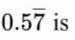
a) 26/45
b) 57/99
57/100
d) None of these
5. In the given graph, the number of student who scored 60 or more marks is
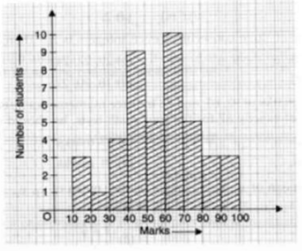
a) 22
b) 20
c) 21
d) 19
6. The equation x = 7 in two variables can be written as
a) 1.x + 1.y = 7
b) 1.x + 0.y = 7
c) 0.x + 1.y = 7
d) 0.x + 0.y = 7
7. If ΔPQR ≡ ΔEFD, then ∠E =
a) None of these
b) ∠P
c) ∠Q
d) ∠R
8. Which of the following is a polynomial?
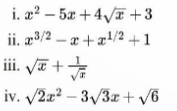
a) Option (iv)
b) Option (ii)
c) Option (i)
d) Option (iii)
9. In a quadrilateral ABCD, AO and BO are the bisectors of ∠A and ∠B respectively, ∠C = 70° and ∠D = 30°. Then ∠AOB = ?
a) 100°
b) 50°
c) 80°
d) 40°
10. If 102y = 25, then 10-y equals
a) -1/5
b) 1/5
c) 1/625
d) 1/50
11. Every rational number is
a) an integer
b) a real number
c) a natural number
d) a whole number
12. In fig. AOB is a straight line. If ∠AOC + ∠BOD = 85°, then ∠COD =
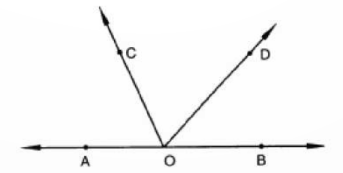
a) 100°
b) 85°
c) 90°
d) 95°
13. Express ‘x’ in terms of ‘y’ in the equation 2x – 3y – 5 = 0

14. If x = 7 + 4√3 and xy = 1, then 1/x2 + 1/y2 =
a) 194
b) 134
c) 1/49
d) 64
15. Which of the following points lies on the line y = 2x + 3?
a) (2, 8)
b) 5,15)
c) (3, 9)
d) (4, 12)
16. In the given figure, if ∠ABC = 45, then ∠AOC =
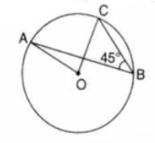
a) 75°
b) 45°
c) 90°
d) 60°
17. Which of the following pair is a solution of the equation 3x – 2y = 7?
a) (-2, 1)
b) (1, -2)
c) (5, 1)
d) (1, 5)
18. Assertion (A): If the angles of a quadrilateral are in the ratio 2:3:7:6, then the measure of angles are 40°, 60°, 140°, 120° respectively.
Reason (R): The sum of the angles of a quadrilateral is 360°.
a) Both A and R are true and R is the correction explanation of A
b) Both A and R are true but R is not the correct explanation of A.
c) A is true but R is false.
d) A is false but R is true
19. If x – 2 is a factor of x2 + 3ax – 2a, then a =
a) 1
b) -1
c) 2
d) -2
20. Assertion (A): 5 – √2 = 5 – 1.414 = 3.586 is an irrational number.
Reason (R): The difference of a rational number and an irrational number is an irrational number.
a) Both A and R are true and R is the correct explanation of A
b) Both A and R are true but R is not the correct explanation of A
c) A is true but R is false
d) A is false but R is true.
SECTION B
21. Solve the equation u – 5 = 15 and state the axiom that you use here.
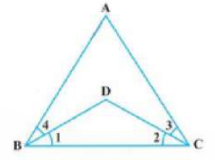
22. In the given figure, we have ∠ABC = ∠ACB, ∠4 = ∠3. Show that ∠1 = ∠2
23. Write the quadrant in which it lies (-7, -4)
24. The ratio of the volumes of the two cones is 4:5 and the ration of the radii of their bases is 2:3. Find the ratio of their vertical heights.
OR
Find the length of cloth used in making a conical pandal of height 100 m and base radius 240 m, if the cloth is 100π wide.
25. Simplify: (3√5 – 5√2)(4√5) + 3√2)
OR
Evaluate after rationalizing the denominator of 25/(√40 – √80) it being given that √5 = 2.236 and √10 = 3.162.
SECTION C
26. The following table gives the number of students in Class IX in a school during academic years 1996 – 1997 to 2000 – 2001

Represent the above data by a bar graph.
27. Simplify:
28. ABCD is a parallelogram AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively.
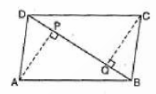
Show that:
i. ΔAPB ≅ ΔCQD
ii. AP = CQ
29. The following table gives the quantity of goods (in crore tonnes)
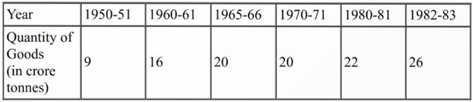
Represent this information with the help of a bar graph. Explain through the bar graph if the quantity of goods carried by the Indian Railways in 1965-66 is more than double the quantity of goods carried in the year 1950-51.
OR
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:

Draw a bar graph to represent the polling results.
30 Find at least 3 solutions for the following linear equation in two variables:
2x + 5y = 13
31. Find the remainder when x3 + 3×2 + 3x + 1 is divided by x + π
SECTION D
32. A right angled triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of the double cone thus generated.
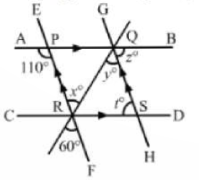
33. In the given figure, AB || CD and EF || GH, find the values of x, y, z and t
OR
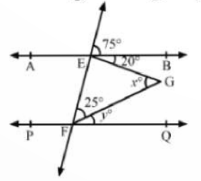
In the given figure, AB || PQ, find the value of x and y.
34. The base of a triangular field is three times its altitude. If the cost of sowing the field at Rs. 58 per hectare is Rs 783, find its base and height.
OR
Find the percentage increase in the area of a triangle if its each side is doubled.
35. Using factor theorem, factorize the polynomial: x4 + 10x3 + 35x2 + 50x + 24
SECTION E
36. Read the text carefully and answer the questions:
As shown in the village of Surya there was a big pole PC. This pole was tied with a strong wire of 10 m length.
Once there was a big spark on this pole, thus wires got damaged very badly. Any small fault was usually repaired with the help of a rope which normal board electricians were carrying on bicycles.
This time electrician need a staircase of 10 m so that it can reach at point P on the pole and this should make 60 with line AC.
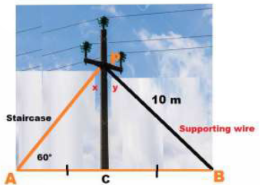
(i) Show that ΔAPC and ΔBPC are congruent.
(ii) Find the value of ∠x.
OR
Find the value of ∠y.
(iii) What is the value of ∠PBC?
37. Read the text carefully and answer the questions:
Ajay is writing a test which consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while ¼ mark is deducted for every wrong answer. Ajay knew answers to some of the questions. Rest of the questions he attempted by guessing.

(i) If he answered 110 questions and got 80 marks and answer to all questions, he attempted by guessing were wrong, then how many questions did he answer correctly?
(ii) If he answered 110 question and got 80 marks and answer to all questions, he attempted by guessing were wrong, then how many questions did he guess?
(iii) If answer to all questions he attempted by guessing were wrong and answered 80 correctly, then how many marks he got?
OR
If answer to all questions he attempted by guessing were wrong, then how many question answered correctly to score 95 marks?
38. Read the text carefully and answer the question:
The principal of a school decided to give badges to students who are chosen for the post of Head boy, Head girl, Prefect and Vice Prefect. Badges are circular in shape with two colour area, red and silver, as shown in figure. The diameter of the region representing red colour is 22 cm and silver colour is filled in 10.5 cm wide ring.
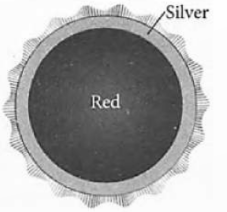
(i) Find the radius of circle representing the red region.
(ii) Find the area of the red region.
OR
Find the area of the silver region.
(iii) Find the radius of the circle formed by combining the red and silver region.