Kindly share you feedback about the website – Click here
Mathematics
Class – IX
Time Allowed: 3 hours Maximum Marks: 80
General Instructions:
1. This question paper contains two parts A and B
2. Both Part A and Part B have internal choices
Part – A:
1. It consists of two section I and II
2. Section I has 22 questions. Internal choices provided in 7 questions.
3. Section II has Q.23 and 24 two case study-based questions. Each case study has 5 case –based sub parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B:
1. Question No 25 to 31 are Very Short Answer type questions of 2 marks each
2. Question No 32 to 38 are Short Answer type questions of 3 marks each
3. Question No 39 to 41 are Long Answer type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part – A
Section – I
1. Every rational number is a _____________
OR
Write the simplest form of a rational number 177/413
2. Write the point where the graph of the linear equation 2x + 3y = 6 cuts the y-axis.
3. Find the value of 2492 – 2482
4. What is the form of any solution of the linear equation 2x + 0y + 9 = 0 in two variables?
5. What are the facts or information collected with definite purpose called?
6. If one angle of a triangle is equal to the sum of the other two angles, then write the type of the triangle.
OR
An exterior angle of a triangle is 80 and two interior opposite angles are equal. What will be the measure of each?
7. AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, then find the distance of AB from the centre of the circle.
8. The quadrilateral PQRS, rhombus if diagonals of PQRS are _____________
9. If the radius of a sphere is 3r, then find its volume.
OR
In a right circular cone, height radius and slant height do not always be sides of a right triangle. Justify.
10. Is it correct to say that in histogram, the area of each rectangle is proportional to the class size of the corresponding class interval. Justify.
11. The ____________ of an equilateral triangle are equal in length.
12. Find the value of 2560.16 x 2560.09
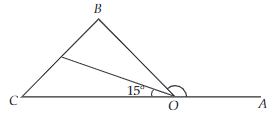
13. In ΔCOB, PO is bisecting of angle ∠COB, ∠COP is given 15, find the ∠BOA.
14. In an equilateral triangle ABC, D and E are the midpoints of sides AB and AC respectively, then find the length of DE.
15. Write the coefficient of x2 in the expansion of (x – 2)2
OR
Write the zeroes of the polynomial p(x) = x(x – 2)(x – 3)
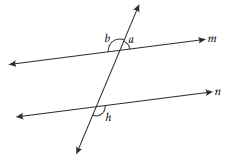
16. In fig, m || n and ∠a : ∠b = 2 : 3, then what will be the measure of ∠h?
OR
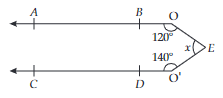
In the given figure, AB and CD are parallel to each other, then calculate the value of x
17. The points P(a, b) lies in the IV quadrant. Find which of a or b is greater?
OR
If the coordinates of the two points are P(-2, 3) and Q(-3, 5), then find the value of (abscissa of P) – (abscissa of Q)
18. How many number of dimensions a surface has?
OR
How many inter-woven isosceles triangles are mentioned in Sriyantra (in the Atharava Veda)
19. Write the angle which is one fifth of its complement.
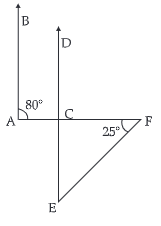
20. In the given figure, AB || CD. If ∠CAB = 80 and ∠EFC = 25, then find ∠CEF.
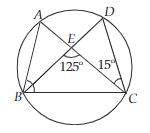
21. In the given figure A, B, C and D are four points of a circle. AC and BD intersect at a point E such that ∠BEC = 125 and ∠ECD = 15. Find ∠BAC
22. In the given figure, ABCD is cyclic quadrilateral in which ∠A = 3x + 30 and ∠C = 2x + 20, then find the value of x
Section – II
23. Five friends Himika, Anjali, Aman, Lakshay and Tarun are standing at the corners P, Q, R, S and T respectively as shown below:
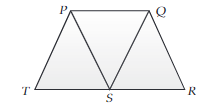
such that PS = ST = PT and QS = SR = QR. Also, triangle PQS is an equilateral triangle.
Answer the following questions:
A) How many equal sides are there in an equilateral triangle?
i) 2
ii) 3
iii) 0
iv) 4
B) How many equilateral triangles are there in the given figure?
i) 1
ii) 2
iii) 3
iv) 4
C) Which statement is incorrect for the given figure?
i) ∠T = ∠R
ii) ∠QPT = 120
iii) It has a scalene triangle
iv) PT = QS
D) Name the axioms by which ΔPTS and ΔQRS are not congruent.
i) SAS
ii) SSS
iii) RHS
iv) None of the above
E) If PT = 2x + 1 and QR = 3 – 2y, then find the relation between x and y
i) x + y = 1
ii) x = y
iii) 2x = y
iv) x/y = 2
24. Beti Bachao, Beti Padhao (BBBP) is a personal campaign of the Government of India that aims to generate awareness and improve the efficiency of welfare services intended for girls.

In school, a group of (x + y) teachers, (x2 + y2) girls and (x3 + y3) boys organised a campaign on Beti Bachao, Bedi Padhao.
A) Which mathematical concept is used here?
i) Linear equations
ii) Triangles
iii) Polynomials
iv) Area
B) Which is the correct identity?
i) (a + b)2 = a2 + b2 + 2ab
ii) (a + b)2 = a2 + b2 + 2ab
iii) (a + b)2 = a2 – b2 – 2ab
iv) All are correct
C) (x – y)3 =
i) (x2 – y2 – 3xy(x – y))
ii) x3 – y3 – 3xy(x – y))
iii) (x3 – y3 – 2xy(x – y))
iv) (x3 – y3 – 3xyx – y)
D) If in the group, there are 10 teachers and 58 girls, then what is the number of boys?
i) 300
ii) 360
iii) 350
iv) 370
E) Using part (D), find (x2 – y2) if x – y = 23
i) 200
ii) 330
iii) 120
iv) 230
Part – B
25. Express y in terms of x from the equation 3x + 2y = 8 and check whether the point (4, -2) lies on the line.
26. In the figure, OA = OB and OD = OC. Show that:
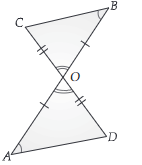
i) ΔAOD ≅ ΔBOC
ii) AD || BC
OR
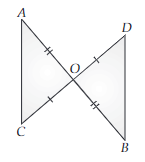
In the figure below, O is the midpoint of AB and CD, prove that AC = BD
27. If the area of an equilateral triangle is 81√3 cm2. Find its perimeter.
28. In the figure below, the diagonal AC of quadrilateral ABCD bisect ∠BAD and ∠BCD. Prove that BC = CD
29. Find the value of ‘a’ for which (x – 1) is a factor of the polynomial a2x3 – 4ax + 4a – 1
OR
For what value of k, the linear equation 2x + ky = 8 has x = 2 and y = 1 as its solution?
If x = 4, then find the value of y.
30. Sides of a triangle are 70 cm, 80 cm and 90 cm. Find its area (Use = √5 = 2.23)
31. Five friends playing a game in which they are standing at different positions, P, S, T, R and Q.
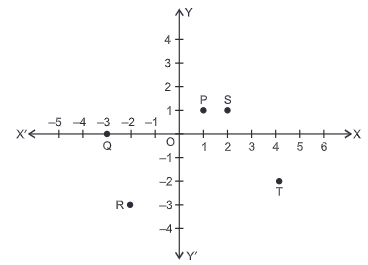
Observe the given figure and answer the following questions:
i) What are the coordinates of P?
ii) Name the point whose y-coordinates is zero.
32. Find six rational numbers between 3 and 4.
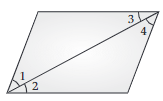
33. In the given figure, if ∠1 = ∠3, ∠2 = ∠4 and ∠3 = ∠4, write the relation between ∠1 and ∠2, using Euclid’s
Solve the equation 2x + 1 = x – 3 and represent the solution(s) on
i) The number line
ii) The Cartesian plane
34. Evaluate 1113, using a suitable identity
35. ABCD is a quadrilateral in which P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that PQRS is a parallelogram.
OR
In ΔABC, D, E and F are the mid-points of sides AB, BC and CA. If AB = 6 cm, BC = 7.2 cm and AC = 7.8 cm, find the perimeter of ΔDEF
36. Write 3x + 2y = 18, in the form of y = mx + c. Draw its graph
37. A birthday cap is in the form of right circular cone of the base radius 5 cm and slant height 13 cm. Find the area of the sheet required to make 50 such caps.
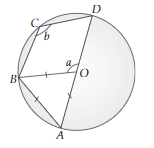
38. In the given figure, AB is a chord equal to the radius of the given circle with centre O. Find the value of a and b.
39. In the given figure, AB || DC, ∠BDC = 35 and ∠BAD = 80, Find x, y, z
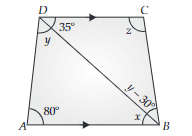
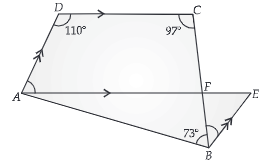
OR
In the below figure ABCD is a quadrilateral in which ∠ABC = 73, ∠C = 97 and ∠D = 110. If AE || DC and BE || AD and AE intersects BC at F, find the measure of ∠EBF.
40. Fahrenheit (F) and Celsius (C) are two different units of temperature and the relation between them is given by C = 5/9(F – 32°). Draw the graph for this relation. At what temperature both units read the same, also find temperature °C which is equal to 30 °F
41. The following tables gives the life of 400 neon lamps:
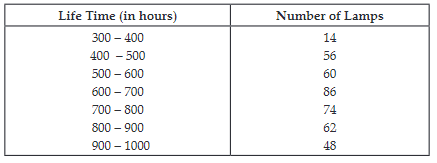
i) Represent the given information with help of histogram
ii) How many lamps have life time of more than 700 hours?